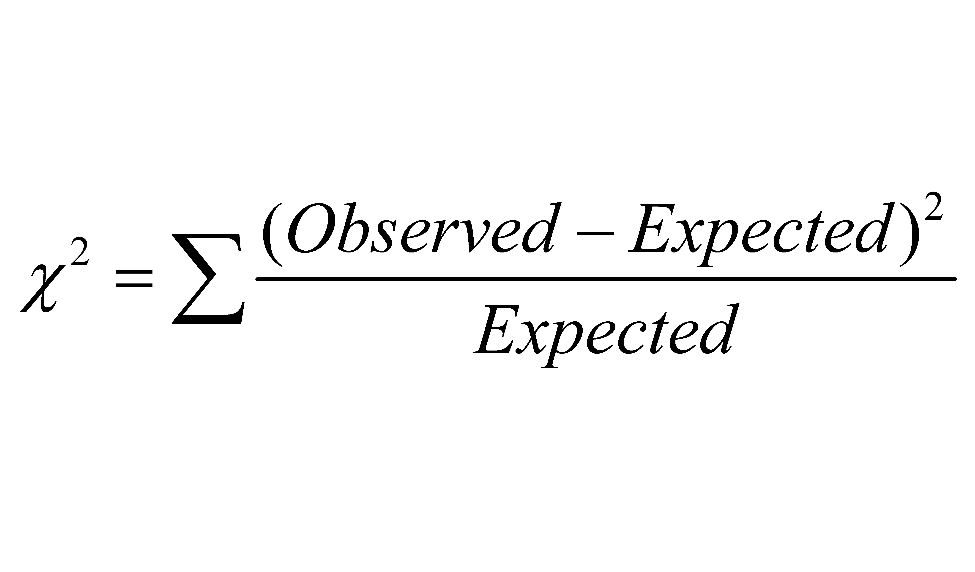 When surveys are done for purposes of research we often would like to know whether there is a relationship between answers to specific questions. As an example, consider a survey conducting research on the motivation for running as a sport. We may hypothesizes that men’s motivation for running is more likely to be related to competing than are women’s motivation. Let’s see how survey questions and responses can help with hypothesis testing.
When surveys are done for purposes of research we often would like to know whether there is a relationship between answers to specific questions. As an example, consider a survey conducting research on the motivation for running as a sport. We may hypothesizes that men’s motivation for running is more likely to be related to competing than are women’s motivation. Let’s see how survey questions and responses can help with hypothesis testing.
Questions related to our hypothesis
Now that we have our hypothesis, which questions would be appropriate to include in our survey? One obvious question would be to indicate the respondent’s gender. A second question may be one which would allow respondents to select their main motivation for running. Let’s take a glimpse of the results:
| Losing weight | Being competitive | Feeling high | Escape from everyday life pressures | |
| Women | 198 | 33 | 75 | 55 |
| Men | 121 | 94 | 61 | 72 |
These results indicate quite clearly that our hypothesis is very likely true. Of those indicating their main motivation for running is being competitive, a much larger percentage are men than are women. The difference is sufficiently large that it’s highly unlikely that the difference is due to chance. We conclude that running motivation is highly likely to be dependent upon (or related to) gender.
How likely is ‘highly likely’?
We are dealing with numbers here. Therefore, it may not come as a surprise there is some kind of mathematical equation that munches the numbers in our table above and spits out some magical number indicating exactly how likely is “highly likely”. Indeed, such a mathematical formula exists. It is called ‘Chi Square’.
The Chi Square method calculates the likelihood of dependency between categories (in our case, gender and running motivation). In fact, the Chi Square method used on the numbers in the above table calculates the probability for a dependency between the two categories as 99.99999%. This is the same as saying that the probability the difference between number of men choosing competitiveness (94) and the number of women (34) is due to chance alone is less that 0.00001%.
For those inclined towards mathematics or statistics and would like to get a more in depth look at how Chi Square works please go ahead and check out one example.
How does OwnSurvey use the Chi Square test?
OwnSurvey displays the likelihood of dependency for each pair of questions contained in your survey. Say, for example, you are interested in whether questions number 7 and 10 in your survey have some sort of dependency. Check out the Contingency Checks report at the cell representing the question pair, i.e., column 7 and row 10. If the value in the cell is just under 100 percent the questions are highly likely to be dependent.
The main method used for this calculation is, as mentioned, the Chi Square test. The Chi Square test requires there be a minimal number of responses to our survey. How many responses do we need? Notice in our table above, there are 8 possible combinations for answering the two questions. Ideally, the survey would receive enough responses so that all combinations of gender and possible answers for other questions receive at least 5 responses. In other words, in our table above, each cell would ideally have a number of at least 5.
What if our responses did not reach the ideal minimum?
If some of the possible combinations were answered by less than 5 respondents, other methods may be used in conjunction with Chi Square:
-
- Fisher’s exact test (See an example)
- Yates correction (See an example)
- Merging category possibilities. To explain this, consider a question that rates how important a new personal record (PR) is for the runner. The question may have a scale of 1 to 4; 1 being ‘not important’ and 4 being ‘very important’. Now, if there aren’t at least 5 responses for each of the 4 ratings, we can aggregate (or merge) ratings 1 and 2 and label them “Not important”. Similarly, we aggregate scales 3 and 4 and label them “Important”. Although we end up with only 2 scales, they are still meaningful. Hopefully, each would now include at least 5 responses. Aggregations can occur only for questions of type “radio button scale” or for questions marked as “scale questions”.
Hypothesis testing is easy; watch the short video
The following video shows how to apply hypothesis testing in your surveys. Our hypothesis is the same as discussed above: men’s motivation for running is more likely to be related to competing than are women’s motivation.
The video starts off with an already created survey. The first question asks for the respondent’s gender. The remaining questions ask the respondent to rate certain aspects of running that have to do with a competitive nature. An example is how important are new personal records for the respondent. Notice the last question is marked as a scaled question for any aggregation calculations if necessary. The Contingency Checks report displays a simple numeric value indicating whether our hypothesis tested out true or not.
Happy hypothesis testing!